DIY Electrical Electronics Projects Blog
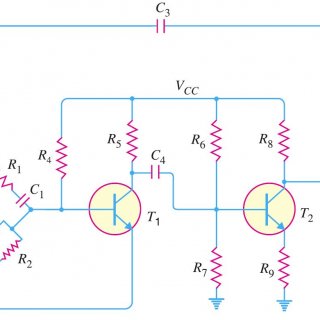
Wien Bridge Oscillator: We have already discussed about various transistor based oscillator circuits in our previous posts. In this short post, let us discuss about How Wien Bridge Oscillator Works? Before proceeding further let...
FET Applications: What are the various applications of the Field Effect Transistor? In this short post let us discuss about the various applications of FET - Field Effect Transistor. Before proceeding further it is...
Tunnel Diode Oscillator: We have already discussed that a tunnel diode is always operated in the negative resistance region. When operated in negative resistance region, the tunnel diode works very well as a oscillator....
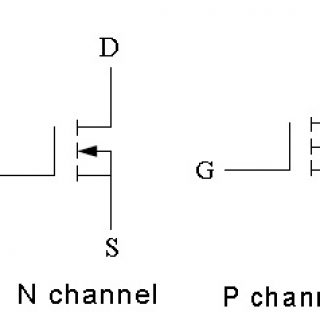
Comparison of N Channel and P Channel MOSFETs The P-channel enhancement MOSFETs were very popular, because it was much easier and cheaper to produce than the N channel device. But now a days these...
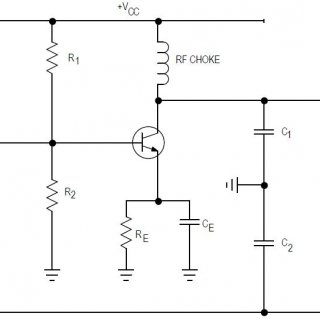
How Colpitt’s Oscillator works? Various commonly used transistor based oscillator circuits are Tuned collector Oscillator Colpitt’s Oscillator Hartley Oscillator Phase Shift Oscillator Wien Bridge Oscillator Crystal Oscillator All these oscillators have the same function...
Relation between Electrical and Thermal Units: In this short post let us discuss about the relation between Electrical and Thermal Units. Joule's Law of Electric Heating: The amount of work done or energy required to...